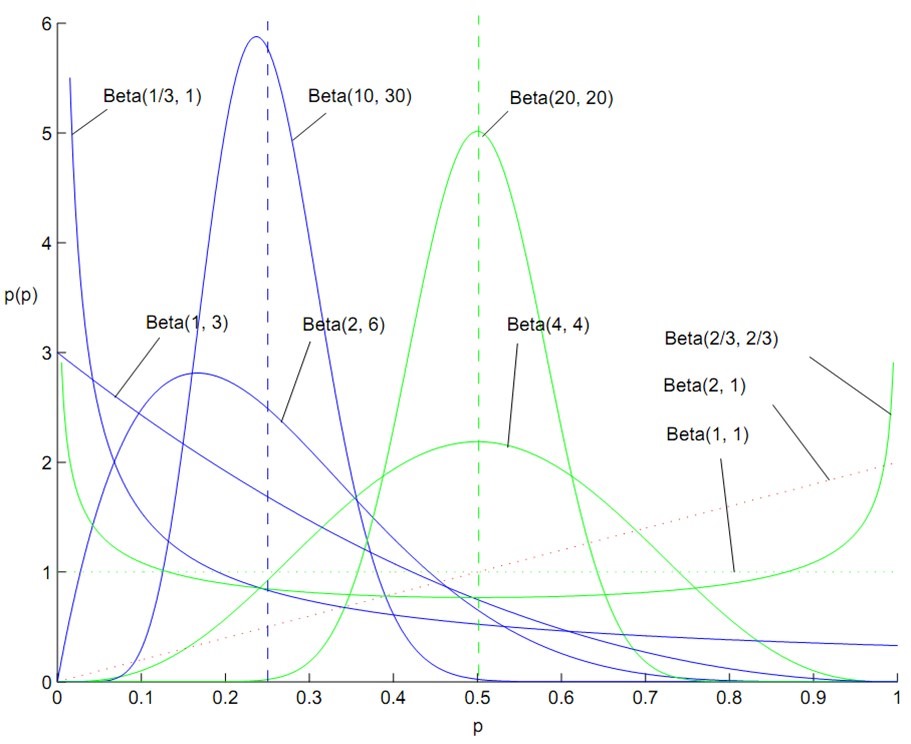
似然函数的计算实例

似然函数的计算实例

考虑投掷一枚硬币的实验。假如已知投出的硬币正面朝上的概率是 ，便可以知道投掷若干次后出现各种结果的可能性。比如说，投两次都是正面朝上的概率是0.25：

从另一个角度上说，给定“投两次都是正面朝上”的观测，则硬币正面朝上的概率为的似然是

尽管这并不表示当观测到两次正面朝上时 的“概率”是0.25。如果考虑 ，那么似然函数的值会变大

这说明，如果参数的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设0.5 时更大。也就是说，参数取成0.6 要比取成0.5 更有说服力，更为“合理”。总之，似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。