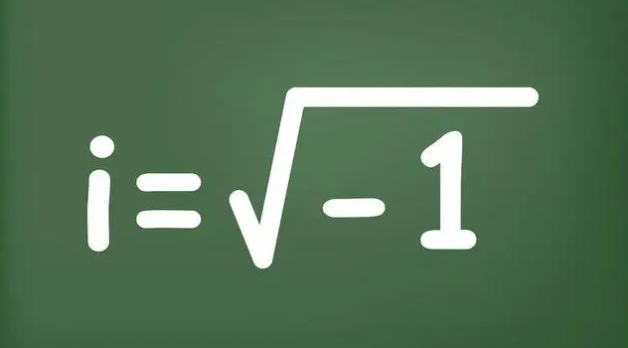什么是套利定价理论

什么是套利定价理论

套利定价理论APT(Arbitrage Pricing Theory) 是CAPM的拓广，由APT给出的定价模型与CAPM一样，都是均衡状态下的模型，不同的是APT的基础是因素模型。套利定价理论认为，套利行为是现代有效率市场（即市场均衡价格）形成的一个决定因素。如果市场未达到均衡状态的话，市场上就会存在无风险套利机会。 并且用多个因素来解释风险资产收益，并根据无套利原则，得到风险资产均衡收益与多个因素之间存在（近似的）线性关系。 而前面的CAPM模型预测所有证券的收益率都与唯一的公共因子（市场证券组合）的收益率存在着线性关系。套利定价理论的出发点是假设证券的回报率与未知数量的未知因素相联系。因素模型是一种统计模型。套利定价理论是利用因素模型来描述资产价格的决定因素和均衡价格的形成机理的。这在套利定价理论的假设条件和套利定价理论中都清楚的体现出来。线性多因素模型的一般表达为:(1)r = a + B * F + ε其中:r代表N种资产收益率组成的列向量.F代表K种因素组成的列向量a是常数组成列向量B是因素j对风险资产收益率的影响程度,称为灵敏度(sensitivity)/因素负荷(factor loading). 组成灵敏度矩阵.ε是随机误差列组成的列向量.并要求:(2)定义：对于一个有N个资产,K种因素的市场,如果存在一个证券组合,使得该证券组合对某个因素有着单位灵敏度,而对其他因素有着零灵敏度. 那么该证券组合被称为纯因素证券组合.rf是无风险收益率,λ每单位灵敏度的某因素的预期收益溢价.纯因素证券组合不只一种，那么这些不同的证券组合，是否会产生同样的期望收益呢？答案是肯定的，这就涉及到无套利均衡。二、无套利均衡（no arbitrage equilibrium）套利和无套利是现代金融的最基本的概念之一.定义: 套利机会(Arbitrage Opportunity)存在一个交易策略,满足以下4个条件:1)不需要任何投入,自我融资(self-financing)lwA = 0　(7)2)对所有因素风险完全免疫BwA = 0　(8)3)对所有非因素风险完全免疫4)当资产数目足够多时,期末可以获得无风险收益无套利原理:在市场均衡时刻，不存在任何套利机会.