什么是方差？

什么是方差？

方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。吵桥改概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与升判全体样本值的平均数之差的平方值的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。

方差是衡量源数据和期望值相差的度量值。

扩展资料

方差是实际值与期望值之差平方的平均值，而标准差是方差算术平方根。 [5]  在实际计算中，我们用以下公式计算方差。

方差是各个数据与平均数之差的平方的和的平均数，即

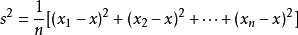
，其中，x表示样本的平均数，n表示样本的数量，xi表示个体，而s^2就表示方差。

而当用

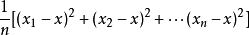
作为样本X的方差的估计时，发现其数学期望并不是X的方差，而是X方差的

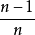
倍，

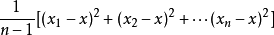
的数学期望才是X的方差，用它作为X的方差的估计具有“无偏性”，所以我们总是用

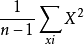
来估计X的方差，并且把它叫做“样本方差”。

方差是和中心偏离的程度，用来衡量一批数据的波动大小（即这批数据偏离平均数的消春大小）并把它叫做这组数据的方差，记作S2。 在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。

公式可以进一步推导为：

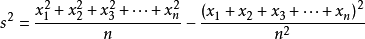
。其中x为这组数据中的数据，n为大于0的整数。

参考资料方差_百度百科