子集与真子集的区别(举例说明)

子集与真子集的区别(举例说明)

子集与真子集的区别是包含的范围不同。

1、子集是一个集合中的全部元素是另一个集合中的元素，有可能与另一个集合相等。

例如：设全集I为{1, 2, 3}，则它的子集可以是{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}、{1, 2, 3}、∅。

2、真子集是一个集合中的元素全部是另一个集合中的元素，但不存在相等。

设全集I为{1, 2, 3}，则它的真子集为{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}、∅。

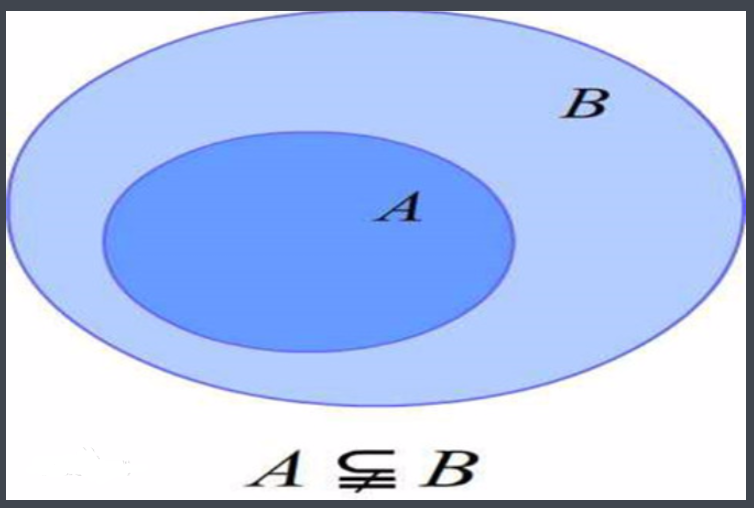
扩展资料：

设S，T是两个集合，如果S的所有元素都属于T ，即 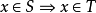 则称S是T的子集，记为  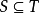。显然，对任何集合S ，都有  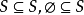。其中，符号  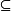读作包含于，表示该符号左边的集合中的元素全部是该符号右边集合的元素。

如果S是T的一个子集，即 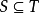 ，但在T中存在一个元素x不属于S ，即  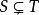，则称S是T的一个真子集。

集合在数学领域具有无可比拟的特殊重要性。集合论的基础是由德国数学家康托尔在19世纪70年代奠定的，经过一大批科学家半个世纪的努力，到20世纪20年代已确立了其在现代数学理论体系中的基础地位，可以说，现代数学各个分支的几乎所有成果都构筑在严格的集合理论上。

参考资料来源：百度百科-真子集

参考资料来源：百度百科-集合