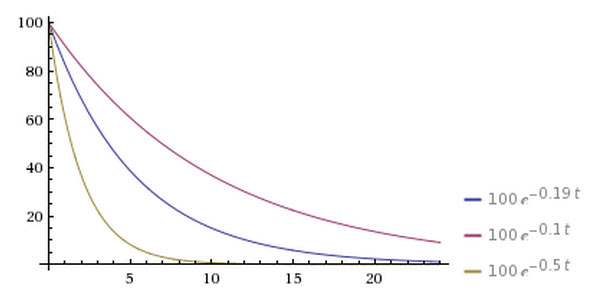
牛顿冷却定律的定义
的有关信息介绍如下:温差Δt=|tw-tf|
q=hΔt
Φ=qA=AhΔt=Δt/(1/hA)
其中的1/hA 称为对流传热热阻 q为热流密度
h为物质的对流传热系数
Φ为传热功率(或者说是单位时间内的传热量)A为传热面积
一个热的物体的冷却速度与该物体和周围环境的温度差成正比。 即-dT/dt=(T-Tc)/τ 式中, -dT/dt——物体的温度随时间下降的速度,负号表示物体的温度是下降的τ——物体的温度从T 下降到环境温度Tc实际所需要的弛豫时间在微分条件下,-dT/dt和(T-Tc)/τ是微线性关系。这是微线性思维的典范之一。
牛顿冷却定律的这个微分方程没有考虑物体的性质,所以这不是物性方程式。它只是关于一个假想物体,其温度随时间单纯下降的一个数学微分方程。与其叫“牛顿冷却定律”,毋宁叫“牛顿冷却定理”更准确。不过,这个明显的缺点,反而是最大的优点。它的无比抽象性在宣告:“这是任何物体冷却的共同遵守的数学规律!”。 物体的温度随时间下降的速度和物体的结构以及理化性质并非完全无关。尤其是急速冷却的条件下,我们可以修改线性“牛顿冷却定理”,给它添加若干个非线性的项就可以解决实际问题了。
这也告诉我们上面的微线性牛顿冷却定律至少不适用于描写那些急速温度变化的物理现象。
解方程可得牛顿冷却定律的积分形式为
Δt=t-to=τln(To-Tc)/(T-Tc)
或者 exp(Δt/τ)=To-Tc/T-Tc
式中,To——为物体在初始时刻to的温度
Δt>0,这是必然的。为此,必然有 To>T>Tc。
这就是说,物体的起始温度To必然大于它最后的冷却温度T;物体最后的冷却温度T不能比环境温度Tc更低,而且也不能被冷却到和环境温度一样低。我们可以假设最后的冷却温度非常接近环境温度,
这时,T-Tc=ΔT,ΔT>0,且ΔT→0。也就是说,温度ΔT是一个极小的正值。
设热水的冷却方程为:exp(Δt/τ)=To-Tc/T-Tc
设冷水的冷却方程为:exp(Δt`/τ`)=To`-Tc`/T`-Tc`
假设,热水和冷水的起始时刻一致to=to`,冷却的环境温度一致Tc=Tc`,热水比冷水的起始温度高,To>To`,热水和冷水最后的状态几乎一致,即热水和冷水最后的温度与环境的温度差无穷逼近——即近似相等,ΔT=T-Tc=ΔT`=T`-Tc。
热水和冷水方程之比:exp(Δt/τ)/exp(Δt`/τ`)=To-Tc/To`-Tc
=exp(C)>1(即 C>0)
于是,Δt/τ - Δt`/τ` = C
Δt=(τ/τ`)Δt`+ C
这是一个截距和斜率都为正值的直线方程,
如果热水比冷水先结冰,Δt<;Δt`,必须有 τ<;τ`。即斜率τ/τ`<1。
如果冷水比先热水结冰,Δt>;Δt`,必须有 τ>;τ`。即斜率τ/τ`>1。
这个结果表明:牛顿冷却定律并不能直接用来判断热水和冷水谁先结冰。
而且热水和冷水无论谁先结冰,都不会影响牛顿冷却定律的正确性。