偏导数是什么？它和导数有什么区别？

偏导数是什么？它和导数有什么区别？

偏导数是将一元函数的导数推广到多元函数，我们知道，导数是函数的局部性质，函数在一点的导数描述了这个函数在这一点附近的变化率，反映函数变化的快慢。一个多变量函数的偏导数，就是它关于其中一个变量的导数而保持其他变量不变。

区别：

一、一元函数，可导必连续，连续不一定可导。多元函数，偏导数存在不能保证连续。

二、几何意义不同

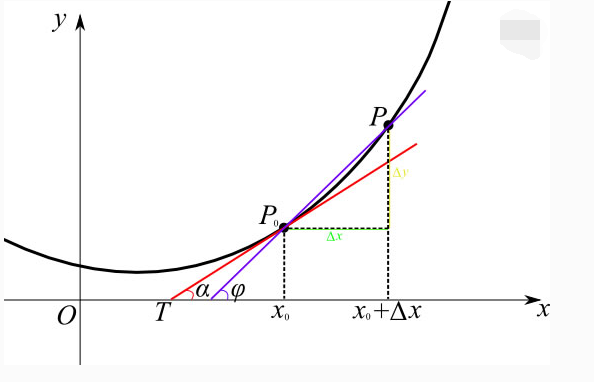
函数y=f（x）在x0点的导数f'（x0）的几何意义：表示函数曲线在点P0（x0,f（x0））处的切线的斜率（导数的几何意义是该函数曲线在这一点上的切线斜率）。

偏导数 f'x(x0,y0) 表示固定面上一点对 x 轴的切线斜率；偏导数 f'y(x0,y0) 表示固定面上一点对 y 轴的切线斜率。

扩展资料

求法：

当函数 z=f(x,y) 在 (x0,y0)的两个偏导数 f'x(x0,y0) 与 f'y(x0,y0)都存在时，我们称 f(x,y) 在 (x0,y0)处可导。如果函数 f(x,y) 在域 D 的每一点均可导，那么称函数 f(x,y) 在域 D 可导。

此时，对应于域 D 的每一点 (x,y) ，必有一个对 x (对 y )的偏导数，因而在域 D 确定了一个新的二元函数，称为 f(x,y) 对 x (对 y )的偏导函数。简称偏导数。

按偏导数的定义，将多元函数关于一个自变量求偏导数时，就将其余的自变量看成常数，此时他的求导方法与一元函数导数的求法是一样的。

参考资料来源：百度百科-偏导数

参考资料来源：百度百科-导数